Estudiar la trayectoria de un disparo determinado, sobre una superficie, es de gran importancia en la Reconstrucción de Hechos ya que puede dar un valor importantísimo al estudio y al esclarecimiento de lo acontecido en la escena, acotando las posiciones posibles en las que se pudo encontrar el arma en el momento del disparo y, por supuesto, excluyendo todas las demás posibilidades utilizando la Geometría cómo base científica.
Determinación de la trayectoria de impacto de proyectiles mediante procedimientos matemáticos.
La balística se estudia según el momento del disparo en el que se encuentre, así, si el proyectil no ha abandonado el cañón, será la interna, si lo abandonó y está en vuelo, es la externa y cuando llegue al objetivo, será el de efecto y también forense. ¿Por qué dos denominaciones?. En el momento de la llegada de la bala, hablando en términos de tiro, es de efecto, pero si nos referimos a los resultados para el informe judicial, será el forense.
En las reconstrucciones de hechos donde han intervenidos armas de fuego, nos encontramos con la necesidad de saber la dirección con la que se produce el o los disparos sobre un objeto, un vehículo, una puerta, un vidrio, etc., para el esclarecimiento del caso en cuestión y para así poder determinar en qué posición y ángulo se encontraba el tirador con respecto al objeto, es decir, la balística de efecto o forense.
Como sabemos, cuando se realiza un disparo sobre un cuerpo se suelen producir dos orificios, uno de entrada y otro de salida.
El método más usado y extendido para determinar la dirección de proyección consiste en introducir una varilla recta por los orificios de entrada y salida con dispositivos láser, que fielmente indica la dirección que tomó el proyectil.
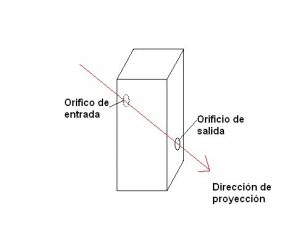
Este método resulta fácil de aplicar cuando el cuerpo atravesado presenta un grosor importante, es decir, cuando entre el orifico de entrada y el de salida existe una buena distancia. Pero ¿Qué ocurre cuando queremos determinar la dirección de proyección sobre una chapa de varios milímetros de espesor, como por ejemplo, la carrocería de un vehículo? En estos casos no sirve para nada introducir las varillas ya que serán muchas las posibles direcciones alrededor de la dirección real. Estaríamos cometiendo grandes errores en la determinación de la trayectoria, ya que tan solo 5º de diferencia en la varilla podrían implicar más de un metro de diferencia en la distancia o la altura de la posición de disparo, con lo cual, la determinación de la posición desde la que se disparó estaría dentro del campo de las conjeturas y nunca se podría afirmar dicha posición.
El método que aquí se presenta se basa en la morfología del orificio de impacto y en las razones trigonométricas para determinar la trayectoria del mismo. Es decir, que estudiando la morfología del orificio y aplicando la trigonometría simple, se puede determinar la dirección con la que se produjo el disparo con un margen de error mínimo.
Para aplicar este método se han de tener en cuenta los siguientes factores:
- Morfología del orificio (circular, elíptica, …)
- Análisis geométrico del orificio (medidas de sus diámetros)
- Tamaño del proyectil
- Inclinación del cuerpo al que se ha proyectado (en vehículos es normal que algunas partes del mismo presenten inclinaciones)
1 – Morfología del orificio
Analizaremos la morfología del orificio, es decir, que debemos comprobar, con un calibre pie de rey, las medidas de los diámetros del orificio a fin de comprobar si es circular o presenta una forma elíptica.
En el caso de que todos los diámetros sean iguales, estamos ante un caso de orificio circular, que sería el más fácil ya que solo ha podido ser provocado con una dirección de proyección ortogonal a la superficie, es decir, que forma 90º con la superficie.
En el caso de que las medidas de los diámetros sean diferentes estamos ante un orificio elíptico y pasaremos al punto 2.
2 – Análisis geométrico del orificio
Ahora debemos encontrar las medidas de los diámetros menor y mayor del orificio elíptico, teniendo en cuenta que si dibujáramos los diámetros mayor y menor éstos formarían 90º uno con respecto al otro tal y como se indica en la siguiente figura:
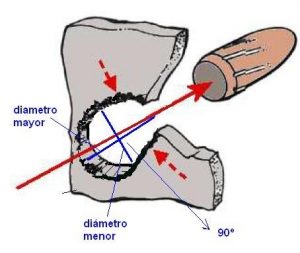
Una vez identificados los diámetros mayor y menor y conocidas sus medidas en milímetros pasamos al punto 3.
3 – Tamaño del proyectil
Ahora necesitamos consultar las bases de datos del fabricante del proyectil para conocer exactamente el diámetro y longitud del proyectil. Por ejemplo, si el orificio anterior hubiera sido efectuado por un proyectil del calibre 9 mm, sabemos que tiene unos 8.92 mm de diámetro de unos 13.36 mm de longitud.
4- Inclinación de la superficie de proyección
Antes de comenzar a hacer el estudio morfo-geométrico es importante establecer si la superficie en la que se encuentra el orificio presenta una inclinación con respecto un plano vertical
imaginario. Esto lo podemos hacer con un simple clinómetro que consiste en una aguja en cuya parte inferior hay un peso, de manera que cuando la superficie es un plano vertical, el clinómetro, que se pega a la superficie, indicaría cero grados y cuando la superficie es un plano horizontal el clinómetro marcaría 90º.

5- Análisis trigonométrico del orificio estudiado
Una vez efectuados los pasos anteriores podemos empezar a hacer un cálculo trigonométrico para poder identificar la dirección con la que se produjo el disparo.
Para realizar el cálculo usaremos la figura del ejemplo anterior. Proponemos que uno de los diámetros sea el eje X y el otro sea el eje Y. Esto lo podemos hacer porque son perpendiculares. En nuestro ejemplo vamos a suponer que el eje X coincide con el diámetro mayor y el eje Y coincide con el menor. Entonces tenemos los siguientes diámetros:
Si el proyectil atravesara el objeto a 90º, es decir, perpendicular a él, el orificio sería un círculo. Sabemos que uno de los ejes, el Y, sí que es de 9 mm, por lo tanto podemos saber que la dirección de proyección forma 90º con respecto al eje Y. Como hemos supuesto que el eje Y es el diámetro menor, podemos afirmar sin temor a equivocarnos que la dirección de proyección es de 90º con respecto a ese eje. Pero ¿Cuántos grados forman la dirección de proyección
con respecto el eje X? Si el proyectil entrara en el cuerpo de forma paralela al mismo, la forma del orificio sería elíptica y con las mismas dimensiones que el proyectil, es decir, que su diámetro menor sería de 8.92 mm y su diámetro mayor sería de 13.36 mm. En la siguiente figura se representa el proyectil con sus medidas y la superficie contra la que impacta pero haciéndolo con distintos grados, concretamente de 10º de 10º.
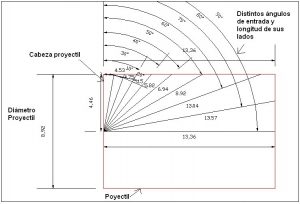
En rojo está representado el proyectil con sus medidas, los arcos representan los ángulos de entrada y las líneas en negro representan los orificios de entrada del proyectil con unas medidas para cada ángulo. Por ejemplo, si el proyectil entra en el objeto con 10º de inclinación la medida de ese diámetro sería el doble de la que se representa en la figura anterior para su radio, el primero de 4.53 mm. Es decir, que un proyectil, de 8.92 mm, que penetra con una inclinación de 10º con respecto a la perpendicular, deja un orificio en ese eje de 4.53 mm de radio, o lo que es lo mismo, 4.53 X2 = 9.06 mm de diámetro. O por ejemplo si el mismo proyectil entra en el cuerpo con una inclinación de 30º con respecto a la perpendicular dejaría un orificio con un diámetro de 5.15 X2 = 10.3 mm. Y así sucesivamente teniendo en cuenta que nunca debemos superar los 13.36 mm que es el tamaño total de la longitud del proyectil. Pero ¿de dónde salen esas medidas de longitud de los radios? Por la trigonometría.
Vamos a coger el triángulo formado por los 4.46 mm del proyectil si el impacto se produjo a 90º y el radio de 4.53 mm que se han medido con el calibre. Entre ambos radios situamos en ángulo α. Usamos la razón trigonométrica del coseno y deducimos que:
cos α = cateto contiguo (4.46) / hipotenusa (4.53)
cos α = 4.46/4.53 ; cos α = 0.984 ; α = arc cos 0.984 = 10.08º
Si nos encontramos con un diámetro de 9.06 mm, es decir, 4.53 mm de radio, podemos afirmar que el ángulo que forma el proyectil con la superficie es de 10.08º. Y este cálculo se hace usando datos que conocemos, como el radio del proyectil y el radio que se ha medido por el orificio de entrada.
Hagamos otro ejemplo:
El diámetro mayor del orificio de entrada tiene una longitud de 11.64 mm y el proyectil es de 8.92 mm de diámetro. Entonces dividimos
11.64 /2 = 5.82 mm de radio, y cogemos los 4.46 mm del radio del proyectil:
cos α = cateto contiguo (4.46) / hipotenusa (5.82)
cos α = 4.46/5.82 ; cos α = 0.766 ; α = arc cos 0.766 = 39.97º =40º
En este caso la dirección del proyectil forma 40º con respecto al del cuerpo que recibe el disparado.
Únicamente existe una incertidumbre con ángulos de proyección muy grandes, es decir, con disparos muy tangenciales. Esta incertidumbre se debe a que según la figura representada a continuación hay una línea, pintada de rosa, que representa un ángulo del que matemáticamente se pude calcular su ángulo, mediante la tangente, pero que usa longitudes superiores a los 13.36 mm de longitud del proyectil, algo que en realidad nunca pasará, ya que nunca dejaremos un orificio mayor que la longitud del propio proyectil. Si calculamos, mediante la tangente, este ángulo, sabremos que estamos hablando de ángulos comprendidos entre 71.54º y 90º. Aunque el de 90º sí que lo conocemos porque abarca justo la longitud del proyectil, 13.36mm.
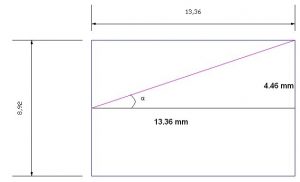
Este abanico de incertidumbre se calcula de la siguiente forma:
Tan α = cateto opuesto (4.46 mm) / cateto contiguo (13.36 mm) =0.333
Α = arc tan 0.333 = 18.46º 90º – 18.46º = 71.54º
Es decir, que desde un ángulo de 71.54º hasta 90º, sin contar 90º que sería cuando el proyectil incide de forma paralela a la superficie, no se podría saber exactamente qué ángulo forma, pero si podemos afirmar que estamos en ese rango de ángulos, que no es poca información. Para el resto de ángulos, desde 0º hasta 71.54º el método es bastante exacto.
JUAN JOSÉ HELLÍN RODRÍGUEZ
Perito en Reconstrucciones de hechos y Balística
Perito en Reconstrucciones de Accidentes de Tráfico Licenciado en Ciencias Experimentales, Experto en Topografía, Fotogrametría y Sistemas de Información Geográfica

